Isomorphism Between SL(2,F4) and A5

A group G is a set of elements along with an operation * that satisfies the following four axioms:

1. Closure 2. Associativity 3. Identity 4. Inverse

One type of group is A Permutation group, representing the permutations of a polygon/platonic solid. The alternating group A5 is the set of permutations of a dodecahedron or icosahedron. It has 60 elements.

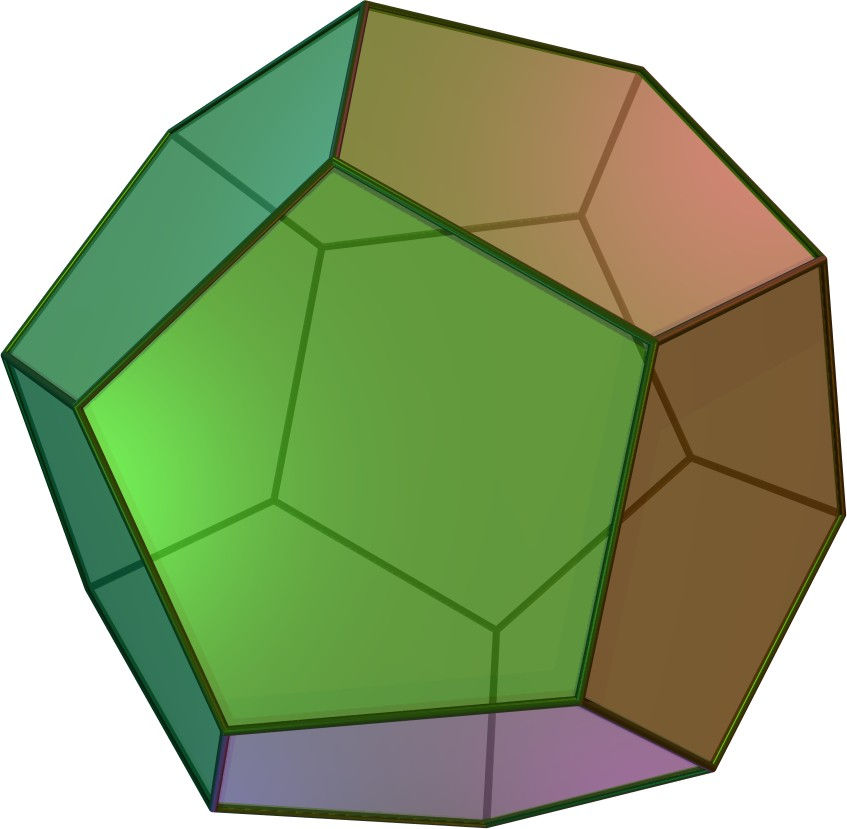
SL(a,F) is the special linear group of a x a matrices whose elements are in field F (i.e. such matrices whose determinant is 1).

This image is not exactly SL(2,F4) but a general idea of what we are talking about.

An isomorphism, in modern algebra, is a one-to-one correspondence (mapping) between two sets that preserves binary relationships between elements of the sets.

If we can map the permutations of the platonic solid to the matrices of the SL group then an isomorphism between the two structures does indeed exist.

This app attempts to do just that, prove that an isomorphism between A5 and SL(2,F4) exists.

Check out the app here.